Teoría de conjuntos (página 2)

Partes: 1, 2

o propios de A
A
3. Conjunto Potencia.- Se llama así al conjunto que esta formado
por todos
los subconjuntos que se forman de un conjunto dado. Se
simboliza por P
su notación P(A), se lee potencia del conjunto A. Ej.:
Hallar la potencia del siguiente conjunto: A= {1, 2,3}
Donde A tiene 3 elementos
P(A)= {{1} ;{2} ;{3} ;{1,2} ;{1,3} ;{2,3} ;{1, 2, 3};Ø}
Donde:
? 23 = 8
n(A)
También si un conjunto tiene “n” elementos, su número de
subconjuntos es 2n
y el número de elementos de sus
subconjuntos propios es 2n -1

Ej.: Hallar el número de subconjuntos y el número de subconjuntos
propios en: B= {f, g, h, i}
P(B)={Ø;{f};{g};{h};{i}:{f,g};{f,h};{f,i};{g,h};{g,i};{h,i};{f,g,h};{f,h,i};

{g, h, i};{f, g, i};{f, g, h, i,}}

El número de elementos de B: n(B)=4

El número de conjuntos potencia de B será:
n[P(B)]= 2n =16

El número de Subconjuntos de B: 16
n

VII.- REPRESENTACIÓN GRAFICA DE CONJUNTO

1.- Diagrama de VENN
Los conjuntos pueden ser representados haciendo uso de gráficas
como: círculos, elipses, rectángulos u otras figuras geométricas de áreas
plana, dentro de los cuales se ubican los elementos que le pertenecen y
fuera a los elementos que no pertenecen al conjunto.

A continuación representamos algunos conjuntos:
A={a,e,i,o,u} y B={a,m,n,o,u}
?AUB={a,e,i,o,u,m,n}
? A n B= {a, o, u}
Nota: “U” es el conjunto universal de todas las letras del alfabeto.

VIII.- OPERACIONES ENTRE CONJUNTOS

Las operaciones de conjuntos son: la unión, la intersección, la diferencia,
la complementación, el conjunto producto y la diferencia simétrica.

1. UNIÓN DE CONJUNTO.- La unión de conjunto A y B es el conjunto
formado por los elementos que pertenecen a A, a B o a ambos, se
simboliza por:
AUB, y se lee “A” unión “B”
Notación:
1)
2)
3)
4)
a
o
u
i
e
m
n
A
B
b
r
U
t
1
2
3
A
B A
B
A
B
1.-Cuando los conjuntos tienen algo en común.
2.-Cuando los conjuntos no tienen nada en común
.

Propiedades: Los más importantes son:

A U B = B U A (conmutativa)
A U A = A (Idempotencia)
A U Ø =A
A U U = U; U: universo
A U B = {x/x ? A ? x ? B}

Gráficamente es:

2.- Intersección (n): Dados lo conjuntos A y B, se llama intersección al
conjunto formado por los elementos que pertenecen a A y B a la vez; es
decir es el conjunto formado por los elementos comunes a A y B
Notación:

Gráficamente:
Propiedades:

i) An B = Bn A
ii) An A = A
iii) A n Ø = Ø
iv) An U = A; U: universo

3.- Diferencia (-): Dados 2 conjuntos A y B, se llama diferencia de A y B, al
conjunto formado por todos los elementos de A y que no pertenecen a B; es
decir, es el conjunto formado por los elementos que pertenecen
exclusivamente a A.
Notación:
A
B
A
B
A
B
.

Ej.: Sean los conjuntos:

A = {1, 2, 3, 6}
B = {2, 4, 6, 7, 8}
C = {4, 7, 8}

? A – B = {1, 3}
B – C = {2, 6}
A – C = {1, 2, 3, 6}
Graficamente:
Gráficamente:
A–B
A–B
A–B

C
A–B= n B
A n B = {X/X ? A Y X ? B}
A – B = {x/x ? A y x ? B}

A
U
Propiedades:
i) A – A = Ø
ii) A – Ø = A
iii) Ø – A = Ø
iv) A – B = B – A ? A = B

4. Complemento de un conjunto (C(A), AC ): Dado un conjunto A que está
incluido en el universo U, se denomina complemento del conjunto A, a
todos los elementos que estén fuera de A, pero dentro del universo.

Notación:
C

Ejem: Sean:

U = {1, 2, 3, 5, 6, 7, 8}
A = {1, 3, 4, 7, 8}
AC = {2, 5, 6}

Gráficamente:
A

Propiedades:

i) (AC) C = A
ii) Ø C = U
iii) U C = Ø
iv) A U AC = U
v) A n AC = Ø

5.- Diferencia Simétrica (?).- Se llama diferencia simétrica de los conjuntos
A y B, al conjunto de elementos de A y B, excepto los que pertenecen a
la intersección. Esto es, que pertenecen a A o a B

A ? B = {x/x ? A y x ? B} v {x/x ? B y x ? A}

NOTA:
PUEDE DECIRSE TAMBIÉN QUE “A ? B” ES EL CONJUNTO DE TODOS LOS ELEMENTOS
DE A B QUE NO PERTENECEN AL CONJUNTO A n B. EN OTRAS PALABRAS “A ? B”
ES EL CONJUNTO FORMADO POR LOS ELEMENTOS “EXCLUSIVOS” DE A O DE B.

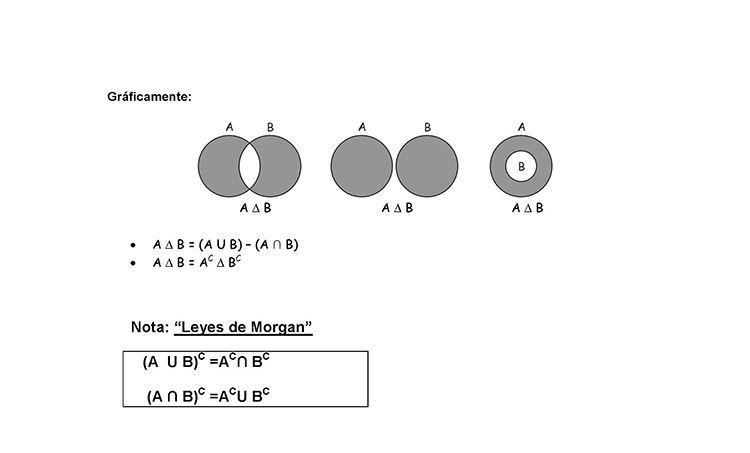
Gráficamente:
A ? B
A ? B
A ? B
•
•
A ? B = (A U B) – (A n B)
A ? B = AC ? BC
Nota: “Leyes de Morgan”

(A U B)C =ACn BC .

(A n B)C =ACU BC